用K-medoids聚类算法检测异常数据
K-medoids聚类算法
K-Medoids 介绍
K-Medoids 是 K-Means 的一种改进版本,用于聚类分析。与 K-Means 不同,K-Medoids 选择实际数据点作为聚类的中心,而不是取均值。这样的中心点被称为“medoids”。
K-Medoids 算法步骤
- 选择初始中心点: 从数据集中随机选择 k 个数据点作为初始中心点。
- 分配数据点到最近的中心点: 对每个数据点,计算其与每个中心点的距离,并将其分配到距离最近的中心点所属的簇。
- 更新中心点(Medoids): 对于每个簇,选择其中一个数据点替代当前的中心点,以最小化该簇中所有数据点到新中心点的距离之和。
- 重复步骤 2 和 3: 重复执行分配和更新步骤,直至簇的分配不再改变或达到预定的迭代次数。
优点
- 对异常值较为鲁棒: 由于中心点是实际的数据点,K-Medoids 对异常值较为敏感,这使得它对于异常值的存在有一定的鲁棒性。
- 适用于离散型数据: 由于 K-Medoids 使用实际数据点作为中心,因此它适用于离散型数据。
K-Medoids 时间复杂度
K-Medoids 算法的时间复杂度取决于其迭代次数和每次迭代的计算成本。总体而言,K-Medoids 是一个迭代的优化算法,其主要步骤包括选择中心点(medoids)和更新簇的分配,直至收敛。
- 选择中心点(初始化): K-Medoids 的初始步骤涉及选择 k 个中心点,这个过程的时间复杂度为 O(kn),其中 n 是数据点的数量。通常,这一步的计算成本取决于选择初始中心点的策略,可能采用随机选择或者其他启发式方法。
- 更新簇的分配: K-Medoids 的主要计算成本在于不断迭代地更新每个点到最近中心点的分配,然后根据这些分配更新中心点。这一步的时间复杂度通常为 O(iter * k * n * d),其中 iter 是迭代次数,k 是簇的数量,n 是数据点的数量,d 是数据点的维度。
- 停止条件: K-Medoids 需要达到收敛条件,通常是簇的分配不再发生变化。停止条件的检查可能涉及对所有数据点的遍历,时间复杂度为 O(n)。
综合考虑,K-Medoids 算法的总体时间复杂度通常在 O(iter * k * n * d) 的数量级,其中 iter、k、n、d 分别是迭代次数、簇的数量、数据点的数量和数据点的维度。
一维数据操作
确定聚类的簇数K
可以通过尝试不同的K值并使用合适的评估指标(如轮廓系数、肘部法则等)来选择最佳的K值。
轮廓系数(Silhouette Coefficient)
Silhouette Coefficient 是一个衡量聚类效果的指标,其值在 -1 到 1 之间。具体而言,对于每个数据点,Silhouette Coefficient 考虑了该点与同簇其他点的相似度和该点与最近的其他簇的点的不相似度。一个高的 Silhouette Coefficient 表示簇内的样本相似度高且簇间的样本相似度低。 在曲线中,轮廓系数越接近1表示聚类效果越好。可以选择具有最高轮廓系数的K值。
肘部法则(Elbow Method)
肘部法则通过绘制不同K值下的聚类模型的损失函数(如簇内平方和)的图形来帮助选择合适的K值。K的选择通常发生在损失函数开始减缓的”肘部”位置。 在图形中,你会看到一个肘部,选择这个肘部对应的K值作为最优的聚类数目。需要注意的是,这个方法并不总是完全明显,有时可能需要主观判断。
一维数据操作代码
数据预处理
1 | # 提取'value'列作为特征 |
确定K值
可以通过尝试不同的K值并使用合适的评估指标(如轮廓系数、肘部法则等)来选择最佳的K值。
1 | # 提取'value'列作为特征 |
训练、执行并进行分析可视化
1 | # 提取'value'列作为特征 |
批量读取文件夹下每个文件,分别训练;将结果保存到文件里,且可视化
1 | import os |
二维数据操作
确定聚类的簇数K
可以通过尝试不同的K值并使用合适的评估指标(如轮廓系数、肘部法则等)来选择最佳的K值。
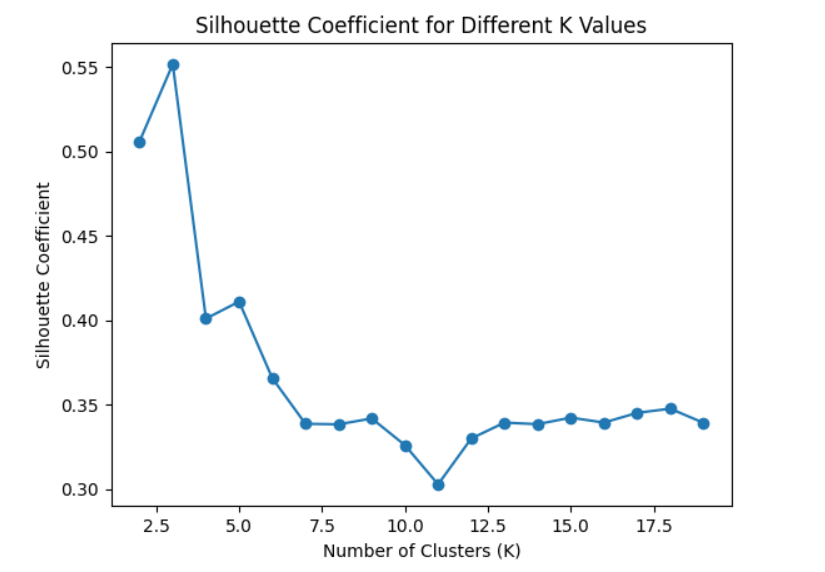
轮廓系数(Silhouette Coefficient)
Silhouette Coefficient 是一个衡量聚类效果的指标,其值在 -1 到 1 之间。具体而言,对于每个数据点,Silhouette Coefficient 考虑了该点与同簇其他点的相似度和该点与最近的其他簇的点的不相似度。一个高的 Silhouette Coefficient 表示簇内的样本相似度高且簇间的样本相似度低。 在曲线中,轮廓系数越接近1表示聚类效果越好。可以选择具有最高轮廓系数的K值。
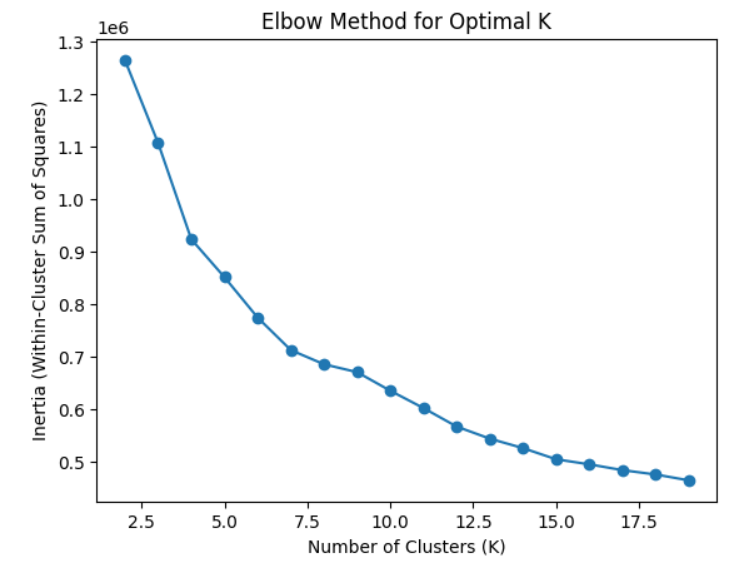
肘部法则(Elbow Method)
肘部法则通过绘制不同K值下的聚类模型的损失函数(如簇内平方和)的图形来帮助选择合适的K值。K的选择通常发生在损失函数开始减缓的”肘部”位置。 在图形中,你会看到一个肘部,选择这个肘部对应的K值作为最优的聚类数目。需要注意的是,这个方法并不总是完全明显,有时可能需要主观判断。
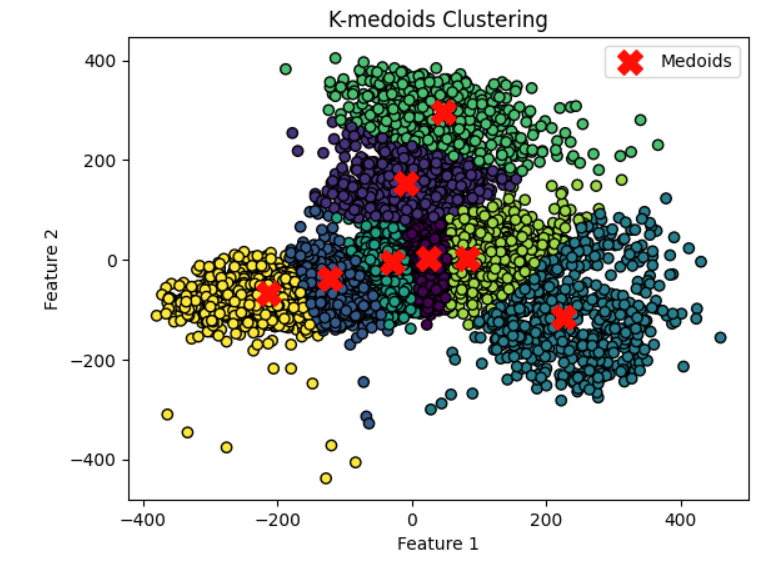
训练-聚类分簇并计算找出异常点
聚类分簇的结果
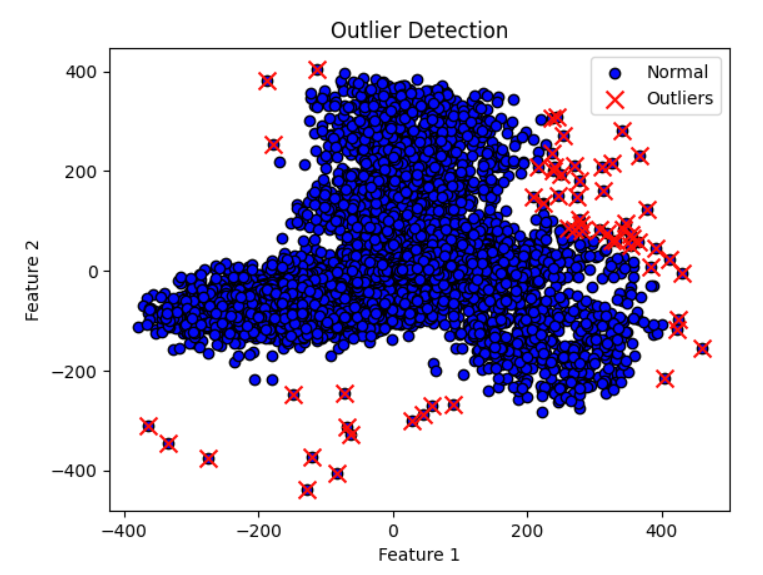
找出异常点的结果
二维数据操作代码
确定聚类的簇数K
可以通过尝试不同的K值并使用合适的评估指标(如轮廓系数、肘部法则等)来选择最佳的K值。
1 | # 转换成二维numpy.ndarray列表 |
使用ChatGPT(单文件执行)
1 | from sklearn_extra.cluster import KMedoids |

